UrbanSim has been at the core of the Urban Simulation Model developed by the CSIR with financial support from the Department of Science and Technology since its inception in 2009. UrbanSim belongs to a class of models developed for the specific purpose of simulating the following subsystems in the urban environment.
The type of model system considered here belongs to the class computational models. A computational model is a mathematical model in computational science that requires extensive computational resources to study the behaviour of a complex system by computer simulation [Wikipedia]. Mathematical models in turn have the distinct advantage of allowing the effects of an individual determining factor to be analysed by keeping all other factors fixed [Wegener (2004)].
While the model system M should be the simplest possible representation of the real world R, it must of course be comprehensive enough to model most of the known factors that could influence land use change. In a comparative study of twenty contemporary urban models Wegener [2004] identified eight important urban subsystems (Figure 2), of which UrbanSim addresses 7. Other models addressed a minimum of two and maximum of eight subsystems.
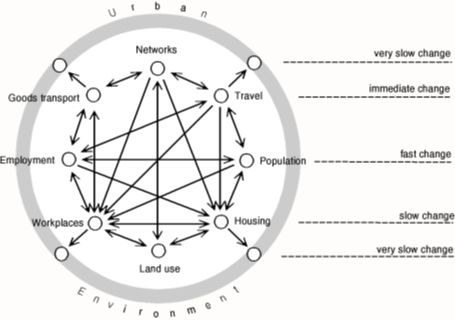
From the perspective of the actors involved in various subsystems one could summarise the above diagram as follows: Households decide where they live, where they work and how they commute between the two. Employment opportunities are created by the location decisions of firms. Developers provide housing and floor space for conducting business after calculating the expected return on investment of development proposals and constructing the proposals that maximise their profit. Government provides transportation networks and regulates physical development by virtue of the rights associated with each parcel of land within a policy environment.
From the perspective of land use, the spatial distribution of residential, business and industrial land uses in particular determines the location of human activities such as living, working and shopping. The spatial distribution of human activities in turn generates trips in the transport system to overcome the distance between the locations of activities. For this reason, the travel and network subsystems are so prominent in urban models that these models are often referred to as Land Use and Transportation (LUT) or Land Use and Transportation Interaction (LUTI) models.
Since UrbanSim does not have an endogenous transportation model it relies on a loose coupling with other models such as MATSim, EMME and VISUM to achieve the desired interaction between land use and transportation. We currently prefer an alternative approach based on OpenTripPlanner.
The literature abounds with a daunting number of available LUT models. As pointed out by Wegener [2004] there are significant variations among the models with respect to comprehensiveness, model structure, theoretical foundations, modelling techniques, dynamics, data requirements and calibration and validation. Based on his latest research findings from the EU-funded SustainCity programme, the primary difference between models can be reduced to:
On a point of disagreement, Wray et al [2013] starts the section on LUT models by stating “These entail aggregate static models …” but later continues with “More recently, a new generation of micro-simulation models that attempt to account for the behaviour and interactions of individual agents in space and time have been developed (Iacono et al., 2008). A few examples of newer LUT models include: UrbanSim (Waddell, 2002), Integrated Land Use Transportation Environment (ILUTE) (Salvani and Miller, 2005) and Integrated Land-Use Modelling and Transport System Simulation (ILUMASS)”. Perhaps it would have been more explicit to state that early LUT models were aggregate and static. Wegener [2013 adapted from Miller 1998] clearly classifies UrbanSim at the pinnacle of disaggregation as shown in Figure 3.
In another review [Wegener et al 2011], UrbanSim is considered as best practice (with two other LUT models: DELTA and IRPUD) in terms of quasi-dynamic models (there are no fully dynamic models available yet) by virtue of subsystem-specific sub models.
From the foregoing it can be concluded that UrbanSim finds itself in an elite group of state of the art models.
The CSIR has also done a significant amount of adaptation to allow UrbanSim to work with different data sources and deal with the phenomena of informal settlements and backyard shacks. Alternatives were investigated to the transportation models that are usually used with UrbanSim and an alternative found in Open Trip Planner. Extensive validations, based on simulating a period in the past were also done to demonstrate that the model can be applied in the South African context.
UrbanSim recognises the property market as the central construct of the urban system and accounts for the current stock of real estate (and its spatial distribution) as well as the supply and demand of new stock. Households and businesses represent the consumers of residential and non-residential stock respectively. The choice of location by these agents is accounted for by the occupation of space in a building.
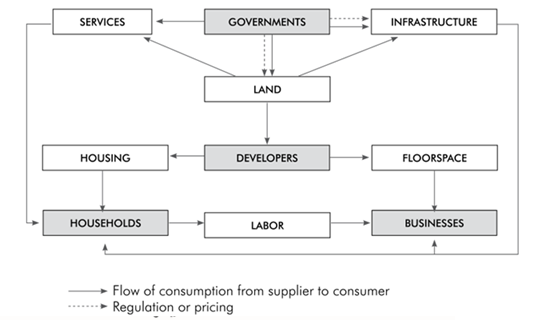
Developer agents, representing the supply side, use occupancy rates as a feedback signal to determine the rate at which new stock can be built and sold. Supply and demand are mediated by price, another feedback signal which influences the return on investment calculation done by developers.
Governments set policies that either regulate the use of land or influence development through pricing policies such as developer contribution fees. Governments also build infrastructure and provide social facilities such as libraries, clinics, community halls, parks, sports field and fire stations. Transportation infrastructure and the quality of social facilities influence the attractiveness of locations for different consumers.
Households have particular characteristics that influence their preferences for housing of different types at different locations. Similarly, businesses have preferences that vary by industry and number of employees for alternative building types and locations. Two models are prominent in modelling these choices, the Household Location Choice Model and the Employment Location Choice Model. Both are discrete choice models based on the pioneering work of McFadden on Random Utility Maximization theory [McFadden, 1974, McFadden, 1981]. This approach determines the probability of a choice from a set of available alternatives based on the characteristics of the chooser and the attributes of the alternatives, depending on the relative utility that an alternative offers the chooser. CSIR implementations consist of five sub models, one for each household income category, with different alternative-specific variables to define the behaviour of households that belong to each income category.
In the Household Location Choice Model for instance, the households that are in the market at a given time were either added by the Household Transition Model or predicted to move by the Household Relocation Model. The model selects all unplaced households (those not associated with a building) and identifies all available housing units within the simulation year. Since the choice sets are generally too large, random sampling of alternatives is used to construct a plausible choice set, where after a Multinomial Logit Model is used to generate location choice probabilities across the choice set for each household. The location probabilities are used with Monte Carlo Sampling to make a determination for each household regarding which of the available locations they will choose. Once a household has chosen a location (building), that location is committed to the household (like a purchase or rental contract) and the residential unit becomes unavailable for any other households, until such time as the occupying household is predicted to move.
Several other models contribute indirectly to location choices by virtue of influencing the relative utility that an alternative offers an unplaced household. The systematic component (as opposed to the random component) of an utility is expressed as a linear combination of estimable coefficients multiplied by independent alternative-specific variables that may be interacted with the characteristics of the household making the choice. Examples of alternative-specific variables that are often used in utility calculations include the price of a property, which comes from the Real Estate Price Model and measures of the time and/or cost of commuting between home and work, which comes from the Transport Model. UrbanSim does not have a built-in transport model but can be linked to a number of external models.
In UrbanSim terms, the term ‘model specification’ amounts to defining a substantial number of alternative-specific variables and estimating (by means of maximum likelihood methods provided by UrbanSim) the coefficients associated with each variable included in the models, from historical data in the database. The choice of variables is more of an art than a science, which starts with those recommended by the UrbanSim manual from urban economic theory. While this is probably true everywhere, the South African context added a few more challenges, such as a negative correlation between low-income households and proximity to work opportunities. Whereas this would defy urban economic theory in a developed country, it is a reality in South Africa due to the politically motivated spatial planning policies of the past.
For more information contact:
Quinton van Heerden, CSIR
qvheerden@csir.co.za